News
Date: 2021-12-30来源:沐曦光启智能研究院科学家 李兆石
前情提要:
异构编程模型系列专栏的最终目的是探索未来的编程模型演化如何适应硬件和软件约束的变化。上一篇“溯洄从之,道阻且长”中,我们回溯了硬件演化中依次碰到的“三堵高墙”:内存墙(1995年)、功耗墙(2005年)和I/O墙(2015年)。本篇将回溯软件约束对编程模型的影响。由于笔者是硬件(芯片)的教育背景,对软件的认知难免会有偏颇,部分论述会用修辞手法来掩饰认知上的缺陷;同时软件的演化脉络根支繁杂,不像硬件那样清晰。因此笔者欢迎大家阅读本篇时,戴着审视的眼镜去批判。
04. 三位一体
在上一篇回溯硬件演化历程时,大家大概已经注意到“摩尔定律”只是给出了一个硬件演化的路径(即芯片上晶体管尺寸不断微缩),而没有给出硬件演化的最终目的。硬件演化的动机是对抗半导体工艺发展中遇到的物理约束。
与硬件不同,软件演化的终极目的早在现代计算机诞生前的阿兰·图灵(Alan Turing)、阿隆佐·丘奇(Alonzo Church)时代就已经经由可计算理论给出。只是这个目的不可达(即希尔伯特第十问题等问题不是可列无穷多次递归可解的)。于是,软件的“圣杯”就像柏拉图的“理念世界”或者康德的“物自体”,对我等凡人而言可远观不可亵玩。即便如此,人类亦已探明了三条接近这一目的的道路:指令式(Imperative)编程语言、函数式(Functional)编程语言、逻辑式(Logic)编程语言;它们分别起源于三种计算模型:以图灵机为代表的随机存取模型(Random Access Machine, RAM)、以Lambda演算为代表的组合子逻辑演算(Combinatory Logic)、以一阶逻辑(First-Order Logic, FOL)为代表的高阶逻辑(备注:FOL能力弱于图灵机和Lambda演算)。数理逻辑学证明了三种计算模型相互等价(即三种模型中一个计算模型可以被任意另一个模型表达)。可以说,这三种计算模型就是软件圣杯的一体三面。

图 1 蹭热点的同时介绍一下本节标题的来源。
三位一体 (Trinity) 原为基督教神学术语:圣父、圣子、圣灵三个不同位格为同一本质。
《黑客帝国》中的崔尼蒂(Trinity)之名亦来源于此。
根据三部曲的剧情,她对于男主Neo也是三位一体的:Midwife, Teacher, Lover。
本节我们将从三个位面分别出发,追溯软件演化历程。沿途我们会打卡goto语句、结构化程序设计、面向对象编程、Lisp、Map-Reduce、Prolog等知名景点。行程紧凑,必有疏漏,还请各位体谅。
4.1 指令式编程语言与图灵机
图灵机不是一台在物理世界实际存在的计算机。它是阿兰·图灵在思考希尔伯特第十问题时的一个思想实验。希尔伯特第十问题又名“判定丢番图方程的可解性”问题:给定一个系数均为整数的、包含任意个未知数的方程,设计一个过程,通过有限次的计算,能够判定该方程是否有整数解。这个描述中的“有限次计算过程”,就是如今计算机科学中“算法”这一概念的雏形。为了解答该问题,图灵、丘奇等数学家开始尝试用数理逻辑严格地定义“算法”。
不幸的是,虽然1900年希尔伯特提出这个问题的目的是激励数学界设计出该问题的求解算法,但是1931年哥德尔不完备定理、1936年的图灵-丘奇论题,一步步地否定了可解希尔伯特第十问题的算法的存在性。通俗地讲,丘奇/图灵先后提出,可计算的问题等价于Lambda演算/图灵机所能计算的问题;而它们能计算的问题都能用可列无穷多次递归来表达。之后的数学家陆续证明,图灵机停机问题、希尔伯特第十问题、连续统假设等等问题,都是不可计算的。篇幅所限本节不再深入介绍不可计算问题,推荐感兴趣的读者阅读《康托尔、哥德尔、图灵——永恒的金色对角线》 [1],其中非常精彩地借用康托尔证明“实数集与有理数集无法一一对应”这一命题时开创的“对角线方法”,揭示了图灵停机问题、罗素悖论、Lambda演算Y组合子的共通本质。
回到我们追溯软件演化历程的主线上。图灵之所以被认为是“现代计算机之父”,不是因为他提出了图灵机或者图灵完备性(Turing-Complete),而是因为他构想了“元图灵机(Universal Turing Machine)” 。
图灵机其实非常类似硬件设计的有限状态机,或者编译原理中的下推自动机(或者想象一个算盘),只是图灵机的状态数量是可列无穷多的:给定一个读写头(如图2左侧所示),一根任意长的纸带,图灵机的计算过程就是让读写头不断地读纸带上的符号,然后根据图灵机内在状态转移规则,改写这个符号,并移动读写头,以进行下一次读;直到读写头读到一个终止符号。可以看出,图灵机就是我们现实中的计算机程序:“纸带”是程序在计算机上执行过程中的状态(算盘上算珠的位置代表的数值);“状态转移规则”是程序的控制流程(拨弄算盘的口诀)。实际上,只要一个编程语言中有用来管理状态的赋值语句,用来表达控制流程的if判断语句、递归或循环结构语句,我们就认为它能表达的程序是等价于图灵机的,也就是图灵完备的(熟悉C++的各位可以思考一下为什么C++ Template是图灵完备的)。
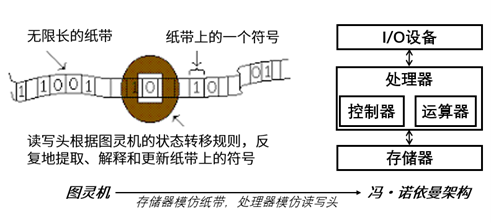
图 2 图灵机与冯·诺伊曼架构
注意,图灵机不是一台现代计算机,而是类似于一个计算机程序,或者一个专用集成电路(ASIC)。二战期间为了破解纳粹德国的Enigma密码,图灵领导一个团队建造的“甜点解码机”,是承接算盘、巴比奇差分机等机械式计算器的巅峰(当时类似的机械式计算器还有用只读的纸带驱动的自动钢琴、织布机等)。所以现代计算机架构不叫“图灵”架构。

图 3 电影《模仿游戏》中复现了图灵与他带队建造的“甜点解码器”
图灵对现代计算机架构的最重要的贡献是他在研究可计算问题时构想的“元图灵机”。所谓元图灵机就是把图灵机当作运算对象的一台图灵机。将一个图灵机的编码T(即图灵机的控制流程)和它的输入数据D交给元图灵机,元图灵机就可以输出T执行D的结果。
在3.1节中,我们曾提到,冯·诺伊曼架构的基本思想是“将计算机指令进行编码后存储在计算机的存储器中”。这里的“计算机指令编码”,实际上就是图灵机的编码T。冯·诺伊曼架构计算的过程,就是让程序和数据都在存储器中以二进制的形式来表示,并由处理器反复地提取、解释和更新(如图2右侧所示)。所以,冯·诺伊曼架构实际上就是元图灵机的工程实现。
面向冯·诺伊曼架构设计的编程语言叫指令式编程语言。它要表达的就是图灵机的编码T。最基础的指令式编程语言是各种处理器体系结构都要定义的汇编语言。根据上文中图灵机的两大基本要素 “状态”和“控制流程”间的相互作用,我们可以分析出所有指令式编程语言的共有指令(或者叫语句):“提取状态”对应读存储器类的指令,“更新状态”对应赋值语句,“状态转移”对应跳转语句,以及用于表达“状态转移规则”的运算语句。
赋值语句是指令式编程语言与其它两类编程语言最根本的区别。目前主流的编程语言都有赋值语句,因此他们都有指令式编程语言的基因。
4.1.1 GOTO语句点燃的结构化程序设计革命
图灵机的控制流程需要根据读入的符号和状态转移规则来移动读写头。这一动作对应的是汇编语言实现控制流的无条件(例如RISC-V的JAL指令)和有条件的跳转(RISC-V的BRANCH)指令。有趣的是,跳转语句在当代编程语言中逐渐消失了:C/C++中还可以用goto语句表明控制流要跳转到源代码中的特定标号;Java中保留了goto关键字,但其语义是在程序员误用C/C++的goto语句时报错;Rust中彻底摒弃goto语句,程序员需要类似功能时只能手写目标体系结构的汇编指令。
摒弃goto语句是软件工程领域结构化程序设计革命的第一步。在硬件和软件工程师还没分家的时代,早期指令式编程语言(如1957年的Fortran)为了贴合硬件思维模式,都会支持goto语句。1968年Edsger Dijkstra的著名文章《goto语句是邪恶的》掀起了结构化程序设计起义。最终起义获得了胜利。1963年的Algol 60语言中最早尝试使用if…else、for、while、switch...case语句作为主要的结构化语法结构。而对于这些语句难以处理的特殊情况,后续编程语言又陆续提供了return, break, continue, exit等语句, 以及异常处理(throw...catch)功能。在这场持续十几年的结构化程序设计革命后,语言设计者最终验证了一个定律:在一个程序中,几乎所有的指令式算法,都可以仅用顺序、分支、选择和循环语句来表达,而不需要goto语句。
结构化程序设计不依赖goto和标号描述控制流,而是依靠词法上嵌套的结构边界作为跳转的目标,例如函数名、if-else、for等语句所在行。1970年Frances Allen将结构边界抽象为控制流图的概念,开创了编译器对指令式编程语言进行自动优化的方法学。从此,程序员不再需要对目标硬件有深入的理解,就可以写出性能不错的程序。而控制流图的概念也将被进一步扩展为“控制-数据流图(Control-Data Flow Graph)”,成为未来编译器设计和数据流体系结构的核心概念。
如今这些结构化程序设计的思想和方法已经让程序员如此地习以为常,以至于大多数人很难想象当年的革命有多么激烈。莺啼破晓,神集新世:1972年图灵奖授予Edsger Dijkstra;1983年图灵奖授予C语言的设计者Ken Thompson和Dennis Ritchie;1984年图灵奖授予Algol-W和Pascal的设计者Niklaus Wirth;2005年图灵奖授予ALGOL 60设计者Peter Naur;2006年图灵奖授予Frances Allen,这也是历史上第一次女性获得图灵奖。今天的我们在翻看图灵奖的获奖记录时,依然能感受到那个激情燃烧的岁月。
4.1.2 从类型抽象到抽象数据类型
图灵机的状态在冯·诺伊曼架构上表示为存储器中的一系列二进制数据。处理器可以按照多种不同方式解释一个二进制数:指令、整数、浮点数、字符串、地址、函数入口……对这些二进制数据进行的分类称为类型 (Type)。对于存储器中哪些位应当如何解释,多数情况下硬件不会预设任何类型,二进制数据本身也不会说明自己的类型。当今的汇编语言中依然可以观察到这种无类型的设计。
与汇编语言不同,高级语言最重要的特征之一就是通过定义类型,将数值与特定的语言结构相关联。由此可以经由类型检查减少程序员构造程序时出错的可能性。例如,如果一个二进制数据被分类为浮点数,那它就不能直接用作存储器地址。类型检查确保了程序员不会将操作应用到无法支持该操作的数据对象上。类型检查可以发生在编译时期,由编译器在进行语义分析时进行静态类型检查,例如C/C++编译器会报类型错误;也可以发生在运行时期,由运行时系统在输入数据被绑定到变量名后进行动态类型检查,例如Python等解释性语言中变量的类型都是在运行时确定的。
20世纪70年代后,随着软件的规模越来越大,开发软件需要的“人月”越来越多(《人月神话》),软件工程学需要对存储器数据的状态也设计一种更结构化的程序设计方法,从而让一个大工程可以被拆分为多个相互正交的子模块。1974年Barbara Liskov提出了抽象数据类型(Abstract Data Type, ADT)的概念,从用户使用数据的方法的视角,而不是数据在存储器中的具体实现,对数据进行分类。例如,只要用户使用入队、出队等操作来操作一段数据,这段数据在ADT视角下就被认为是一个队列,无论这段数据在存储器中是通过链表或是数组或其它数据结构来实现这些操作的。ADT区分了类型的行为和实现,从而即可以防止程序员以不恰当的方式使用存储器的状态,又提高了代码重用的可能性(因为修改模块内部实现时,无需改用使用模块的外部代码)。ADT在十几年后成为了面向对象程序设计的基石。
2009年图灵奖授予了Barbara Liskov。她获奖后有人在网上质疑,模块化和抽象数据类型的概念看起来如此平凡,为啥能拿图灵奖呢?但当我们从历史的视角审视,回到1970年代复杂软件因为混乱的过程描述、泛滥的全局变量而屡屡失败时,我们不仅会感受到开拓者的伟大,更会惊叹于这些概念在今天竟然已经如此深入人心。
如果一种编程模型又通用,又易用,还不会让应用在处理器上的损失过多性能,那这种模型将彻底重构程序员的思考方式,成为一种“润物细无声”的设计,例如结构化程序设计、抽象数据类型等。相对地,如果同一个目的存在两种或多种不同的编程模型,那么这些模型一定是在易用、通用和性能之间存在折衷(Trade-off),例如静态类型检查和动态类型检查之间的张力,就来源于性能和易用性之权衡。
4.2 函数式编程语言与Lambda演算
函数式编程语言对程序构造提供了一个与指令式编程语言迥然不同的视角:它将一个程序的输出定义为其输入的一系列数学函数,且这些函数没有内部状态(等价于C或Java的函数中禁止使用任何赋值语句修改局部或全局变量的状态)。纯粹的函数式编程语言通常被认为bug更少且对形式化验证友好。但由于I/O(例如文件访问、printf等)依赖于赋值语句,以及一些性能上的考虑(因为物理世界的冯·诺伊曼架构处理器是由指令驱动的),主流的函数式编程语言,如Lisp, Scheme, Scala等,都有指令式编程语言的基因;而21世纪后并行编程的需求也让越来越多的指令式编程语言开始杂交函数式性状,如C++11引入的std::function标准库。
函数式编程语言的根源也可以追述到现代计算机出现前的时代。阿隆佐·丘奇,图灵的博士论文导师,在1936年在研究形式化公理系统时,设计了Lambda演算系统。与图灵机对机械计算过程的抽象不同,Lambda演算是用数学的角度对算法进行的抽象:只用了三条构造性语法规则和两条化简规则,就得到了与图灵机等价的计算模型。函数式程序构造是一个树结构:一个函数的输出是一个父节点,其参数是子节点;整个程序的输出是根节点,输入则是所有的叶子节点;化简过程就是从叶子节点出发,一步步地向根节点归并的过程,如图4所示。
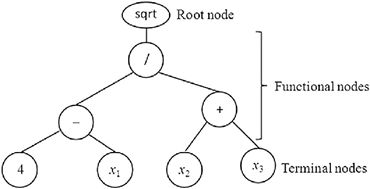
图 4 图中的树表示了函数y=sqrt((4-x1)/(x2+x3))。由于各个函数(父节点)都不会修改状态(即无副作用),
函数求值 (4-x1)和(x2+x3)可以并行执行
函数式编程语言真正进入大众视野还要再等待40年。1977年因为发明FORTRAN语言(今天依然在使用的高级指令式编程语言)而获得图灵奖的John Backus,在他的Turing Award Lecture上做了著名的《程序设计可以从冯·诺伊曼样式中解放出来吗?函数式样式及其程序代数》报告。报告中他提出了“冯·诺伊曼瓶颈”:指令式程序执行每条指令都需要去存储器取指令、提取状态和更新状态,从而使得处理器和存储器之间的数据通路成为性能瓶颈。为了解决该瓶颈,他提出用函数式程序设计思想取代指令式,将程序看作是一种从输入到输出的函数,使用更简单的函数通过逐步细化的过程来定义。由于所有函数都没有内部状态,并且不会修改全局状态,因此程序中有大量函数可以并行求值。70年代后函数式编程语言在学术界产生了巨大的影响:MIT软件设计入门课程6.001及经典教材《计算机程序的构造与解释》(SICP)都采用函数式编程语言Scheme作为大一新生入门程序设计的语言。
但是,产业界中函数式编程却远没有指令式编程应用广泛。一个可能的原因是人的思维模式都是指令式的。当程序员想提高指令式程序的性能时,TA可以很容易地在脑中模拟冯·诺伊曼架构处理器执行指令式程序的过程,从而很快发现性能瓶颈。而当程序员想优化函数式程序的性能时,人脑很难模拟多个函数并行求值的过程。此外,当时所有的处理器体系结构还都是指令驱动的冯·诺伊曼架构。John Backus针对函数式编程语言构想的Parallel Tree架构没有像冯·诺伊曼架构那样的被大众接受,因此程序员也很难将函数式程序与现实中处理器的执行流程建立联系。
4.2.1 MapReduce
直到2004年谷歌的Jeff Dean和Sanjay Ghemawat在OSDI上发表那篇著名的MapReduce论文后,函数式编程方法才真正在产业界创造出巨大的价值。谷歌为了解决大规模分布式计算系统的高并发和容错难题,设计了MapReduce编程模型:程序员使用map函数将对单个元素进行操作的函数扩展到该类元素组成的列表,然后再使用reduce函数对列表中的元素进行归约;这样程序员只需要考虑如何将应用拆分为map和reduce,而不需要关心map和reduce函数具体如何在分布式系统上并发、可靠地实现。
Map, reduce等函数在函数式编程语言中被归类为高阶函数:它们以一个函数作为实际参数,并且可以返回另一个函数。在MapReduce获得成功后,人们又将更多的高阶函数用到分布式系统、多核处理器、甚至FPGA编程上。Python中支持map, filter, reduce;面向数据分析的Python模组Pandas中又进一步加入了groupby, fold等高阶函数;C++11之后的标准库也通过std::function库向程序员提供了自定义高阶函数的能力。
在我看来,高阶函数被广泛接受不是因为函数式编程语言有了何种改进;而是因为随着硬件越来越复杂,软件工程方法学发生了转向。2008年之后,MIT不再开设使用Scheme的6.001作为新生入门课程,转而开设了使用Python的6.0001。当SICP的作者Gerry Sussman 被问到 MIT 为何停掉著名的 6.001 课程时,他指出:“20世纪80年代的软件工程师们通过组合简单并且易于理解的模块的方式来构造复杂系统,但当代软件工程师们的主要工作是为那些他们并不完全理解的复杂硬件写代码。” SICP 及函数式程序设计的目标是在20世纪80、90年代为推导论证复杂系统提供一种抽象语言,而今天大多数程序员学习编程时是在研究如何使用那些巨大的无所不能的程序库满足自己的需求。从这个视角出发,函数式编程语言的高阶函数提供了一种高效且易于理解地将程序库中的函数批量化地应用到大量数据的能力,使得程序员无需考虑数据级并行和容错设计,就能即享受程序库中现成的功能,又享受高并发和分布式系统的性能。归根结底,一种编程语言是否流行,是由特定时期多数程序员思考问题的方式决定的。
4.3 逻辑式编程语言与一阶逻辑
逻辑式编程语言这个名字对于很多程序员而言非常陌生。但其实数据库工程师日常使用的SQL和数字集成电路设计工程师日常使用的设计约束文件(如.sdc),都受到了逻辑式程序设计的影响。篇幅所限本篇不讨论Prolog等通用的逻辑式编程语言,只使用领域定制语言来举例说明。
逻辑式程序设计中,程序员需要表述一组公理和待证明的定理,然后语言的解释器会自动找到推导出定理的过程。例如,SQL查询时公理对应数据表格,定理对应查询目标,解释器则对应SQL query processor;数字集成电路综合使用的约束文件中,公理对应模块及模块间连线的关系,定理对应时序和面积目标,解释器则对应综合器。计算被看作是一种找出满足某特定关系的值(定理)的尝试过程,方法是根据一些逻辑规则(公理)来进行目标导向的搜索。
逻辑式编程语言从一阶(谓词)逻辑中得到灵感。而一阶逻辑的源头比图灵机和Lambda演算更为久远。19世纪末皮亚诺公设成功地形式化了自然数和数学归纳法,之后的数学家将皮亚诺公理系统进一步形式化为了一阶逻辑,并使用一阶逻辑对康托尔集合论进行公理化。这些成果启发了希尔伯特形式化数学的宏伟计划。
1900年,希尔伯特提出了著名的23个问题,多个问题跟形式化和公理化数学证明有关。而其中最著名的希尔伯特第十问题则直接推动了现代计算机的诞生。希尔伯特希望抽离数学证明中的意义,将数学证明抽象成一堆无意义的符号转换。这样,人类证明一个定理所需要的推导,将变成从形式化公理出发的一系列机械式的符号变换。可以看出,逻辑式程序设计利用了形式化公理系统的思想。
函数式和逻辑式编程语言也被统一归类为声明式编程语言。在我看来,“声明式”这个词只是表明了它们不是“指令式”的。除此之外,仅从名称出发我们无法明确声明式编程语言到底是什么(相反指令式编程语言就是用一系列指令对状态的操作来描述应用)。从指令式到函数式,再到逻辑式程序设计,我们可以观察到程序员越来越少地描述程序要怎么做(How),而越来越多地描述程序要做什么(What)。随着当今硬件变得越来越异构,指令式程序设计必将越来越难以理清硬件的复杂性。我可以预见未来流行的编程语言中,函数式、逻辑式程序设计的性状将会越来越多。
本专栏第7篇将继续循着这一视角,审视异构并行编程模型的可能发展方向,包括但不限于函数式程序设计、dataflow model, communicating sequential processes, actor model等等。
番外4:从可计算性反思理性之不完备
“No one shall expel us from the paradise that Cantor has created.
(我们屏息敬畏地自知在康托尔所铺展的天堂里,我们不会遭逢被驱逐的厄运。)
—— 大卫·希尔伯特,1926年
何谓集合?康托尔在1895年作如是说……本书采用通行的Zermelo-Fraenkel公理集合论,并承认选择公理;这套系统简称ZFC……
对于强不可达基数κ,宇宙U:=Vκ连同属于关系∈构成了ZFC系统的一个模型,相当于在集合论内部虚拟地运行了一套集合论。
—— 李文威《代数学方法(第一卷):基础架构》,2019年
一个词怎样起作用,猜是猜不出来的。必须审视它的用法,从中学习。
困难却在于排除阻挡我们这样学习的成见。那可不是笨人的成见。
—— 路德维希·维特根斯坦,《哲学研究》(陈嘉映译本),1945年
上一篇的番外2“从计算机体系结构反思理性建构主义”留下了一个尚未回答的问题:理性(logos)建构主义一定会带来bug吗?对于这个问题,本次番外从对科学数学化的反思出发,给出一个肯定性的理解方向。并在文末指出,logos会出现bug这一观察肯定了人类自由意志的价值。
Logos建构主义的滥觞,可以上溯到牛顿力学后科学的数学化。牛顿力学将数学应用到了经验世界的描述中(如万有引力定律是对开普勒三大定律的公理化描述),并在人类历史上首次成功地用数学演绎推理的能力预言了人类尚未经验之事物(如海王星的发现)。从此人类开始折服于数学的准确性与普遍性。科学革命实际上就是用数学对人类经验到的物理世界进行再描述的过程。在革命过程中,绝大多数受过科学训练的人都成为了柏拉图主义者:相信现象世界和理念世界的分离,相信数学就是那个理念世界中先于经验的真理,是潜藏在事物内部的深度理论。这些理论不可被直接经验到,只有Logos经由数学才能通达。而之后人类对于数学演绎推理的迷信,导出了上篇番外中那个浪漫主义腔调拉满的断言“合乎理性(Logos)的都将变成现实”。
科学革命后,物理学成为科学的典范。数学作为一种先验的真理体系,一步步地从自然科学入侵到社会科学。康德曾断言:“在所有关于自然的特定理论中,我们能够发现多少数学,就能发现多少真正的科学。”哈维将数学引入生理学,孟德尔将数学引入生物学。数学构成了科学的硬核。而在社会科学中,经济学和心理学是数学化的典范,成为最硬核的社会科学;而社会学在经过边沁、密尔等功利主义者不太成功的数学化尝试后,在当今世界的影响力已经远远不如经济学。
为什么数学化有如此大的威力?关键在于数学的普遍性。纯数学要抽离人类经验,转而研究一些不具内涵的符号组成的系统。希尔伯特评述去掉经验内容后的形式化数学,“最后得到的不是用普通语言传达的实质数学知识,而只是含有按照确定规则逐次生成的数学符号和逻辑符号的一组公式而已。于是实质演绎就被一个由规则支配的形式程序替换了。”
数学成为“由规则支配的形式程序”,为数学带来了“进行漫长推理而不失真”的能力 [2]。长程推理的威力不再赘述,相信每一个上过高中物理课的人都会惊叹于天体物理和量子物理中,人类的理性在宏观和微观两个方向上,如何一步步地走到了我们个体经验难以企及的远方。这也正是希尔伯特之形式主义蓝图的创作动机:如果任何一个无矛盾的形式系统所能表达的所有陈述,在该系统中要么能证实要么能证伪,那么所有的数学演绎推理不过是在形式系统中玩文字游戏,可以用纯粹机械的符号变换来完成。如果他的设想成为现实,那么长程推理就不需要一代代天才们筚路蓝缕,而只需要我们在计算机上敲敲手指就可完成。可惜哥德尔、图灵和丘奇等天才最终否定了这种可能。
对数学化的批判有两个视角。其一是数学在描述复杂的现实世界时会失真,这一点在陈嘉映的《哲学·科学·常识》第六章中已有精彩论述。本番外仅用两个笑话来佐证其观点。一个笑话是美剧《The Big Bang Theory》中的“真空中的球形鸡” [3],讽刺数学化的理论物理学依赖过度简化的物理模型,导致它演绎推理出的结论完全不符合经验;另一个笑话则有点让人忧伤:数学化经济学的集大成者,1997年诺贝尔经济学奖获得者,金融模型之父,Black-Scholes模型的提出者之一,Robert C. Merton,曾于1994年和1999年先后两次下场管理对冲基金LTCM和Platinum Grove(其中LTCM合伙人还包括1997年另一位诺奖获得者Myron Scholes),然后在1998年俄罗斯国债违约危机和2008年次贷危机中先后两次破产。
另一个视角则与本篇开头提到的软件“圣杯”相关。希尔伯特第十问题促使丘奇和图灵探索计算的本质。二者分别从形式逻辑和机械计算的角度发现了有些问题无法被有效计算。而不可计算的根源则在于1931年哥德尔博士论文中证明的不完备性定理。所谓不完备性,是说形式系统中存在一个命题,该命题无法在系统内证实或证伪。哥德尔证明了任何强到蕴含皮亚诺公理系统(即一阶逻辑)的一致的(即无内在矛盾的)形式系统都是不完备的。希尔伯特第十问题、图灵停机问题、ZFC公理化集合论是否一致等等问题都是在其对应的形式系统中无法得到证明的问题。
哥德尔不完备性定理击碎了希尔伯特一致且完备地公理化所有数学证明的幻梦:一个完备系统的一致性无法在系统内得到证明;要证明其一致性,需要一个更大的形式系统,而更大的形式系统的一致性又只能由一个更更大的形式系统证明……(是不是很像《黑客帝国》中Matrix与现实的关系)换句话说,我们无法在系统内部同时证明其一致性和完备性,因为“不识庐山真面目,只缘身在此山中”。
哥德尔不完备性定理否定了Logos与机械计算的完备性,同时给人类的自由意志留下了余地。虽然Logos是人类意识的重要组成部分,但在Logos之外,人类意识中有些东西是机械计算无法模拟的,例如有可能亚里士多德之Nous就无法模拟。正是这些东西,让人类可以为了得到一个一致的公理化系统,在系统外用自己创造力增减公理(例如公理化集合论中可以选择是否承认“选择公理”);可以为了看清庐山真面目而选择“更上一层楼”(比如《黑客帝国》中Neo选择吃下红药丸)。也是基于这一观察,彭罗斯在《皇帝新脑》中敢于直言“人工智能的皇帝没有穿衣服”,并断定不存在强人工智能。
可惜的是,人之惰性使得很多时候人们倾向放弃对自由意志的信念,转而去相信生活是由某种难以把握的内在本质所决定。有的人相信阴谋论,认为某个深层政府(deep state)决定了一个TA不认可的国家政策;有的人相信潜意识理论,认为自己难以把控的心理状态是由力比多、阿尼玛/阿尼姆斯等难以获得实证的概念所决定;有的人相信机械决定论,认为自己的所有遭遇都是命定的、被某种难以捉摸的规律所支配的;有的人相信科学拜物教,认为经济基础决定上层建筑,人类社会为了竞争资源必然走向“黑暗森林”,所有TA不能理解的道德情操都是虚伪而无用的。但依然有些人会对自由意志持有信念,并选择以经验主义的、简单明了的观察来对抗那些看似高深、探求内在本质的理论。而这正是维特根斯坦的箴言“不要想,要看”想告诉我们的认识论真相。
下一篇,我们将从一个指令式程序设计的需求出发,探究编程模型如何随着“内存墙”“功耗墙”这两种硬件约束的变化而演化的,并尝试将编程模型的演化规律总结为“三元悖论”。欢迎各位点赞、在看、关注三连。
参考资料

